主要对摄像机成像原理和世界、相机、图像和像素坐标之间的转换关系进行介绍。
四个坐标
理解四个坐标之间的几何关系。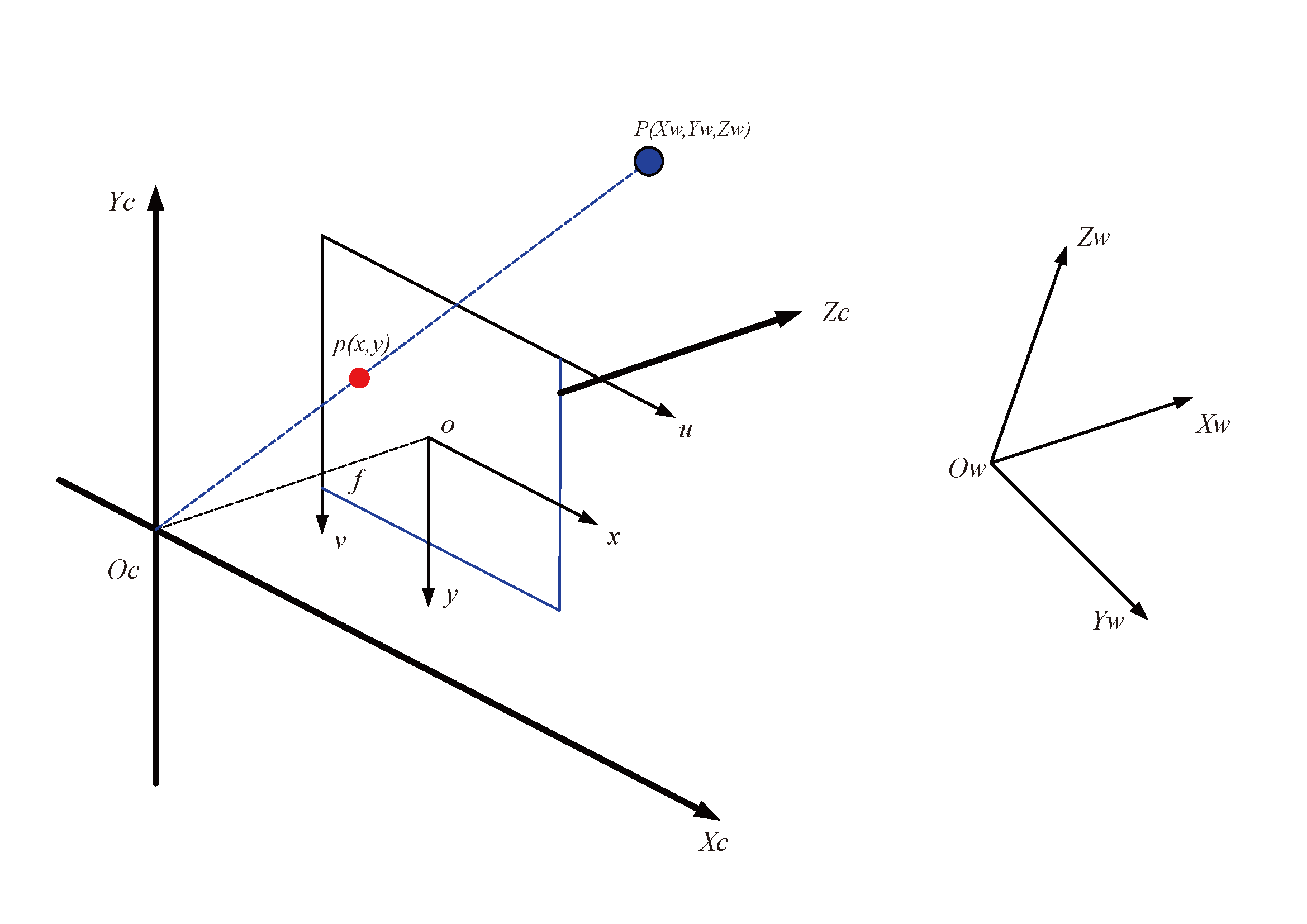
图像处理中涉及到以下四个坐标系:
- $O_w-X_wY_wZ_w$:世界坐标系,描述相机位置,单位:m
- $O_c-X_cY_cZ_c$:相机坐标系,光心为原点,单位:m
- $Oxy$: 图像坐标系,光心为图像中点,单位:mm
- $uv$: 像素坐标系,原点为图像左上角,单位:pixel
- $P$: 世界坐标系中的一点,即为生活中真实的一点;
- $p$: 点$P$在图像中的成像点,在图像坐标系中的坐标为$(x,y)$,在像素坐标系中的坐标为$(u,v)$;
- $f$: 相机焦距,等于$o$与$O_c$的距离,$f=||o-O_c||$。
世界坐标系和相机坐标系之间的转换
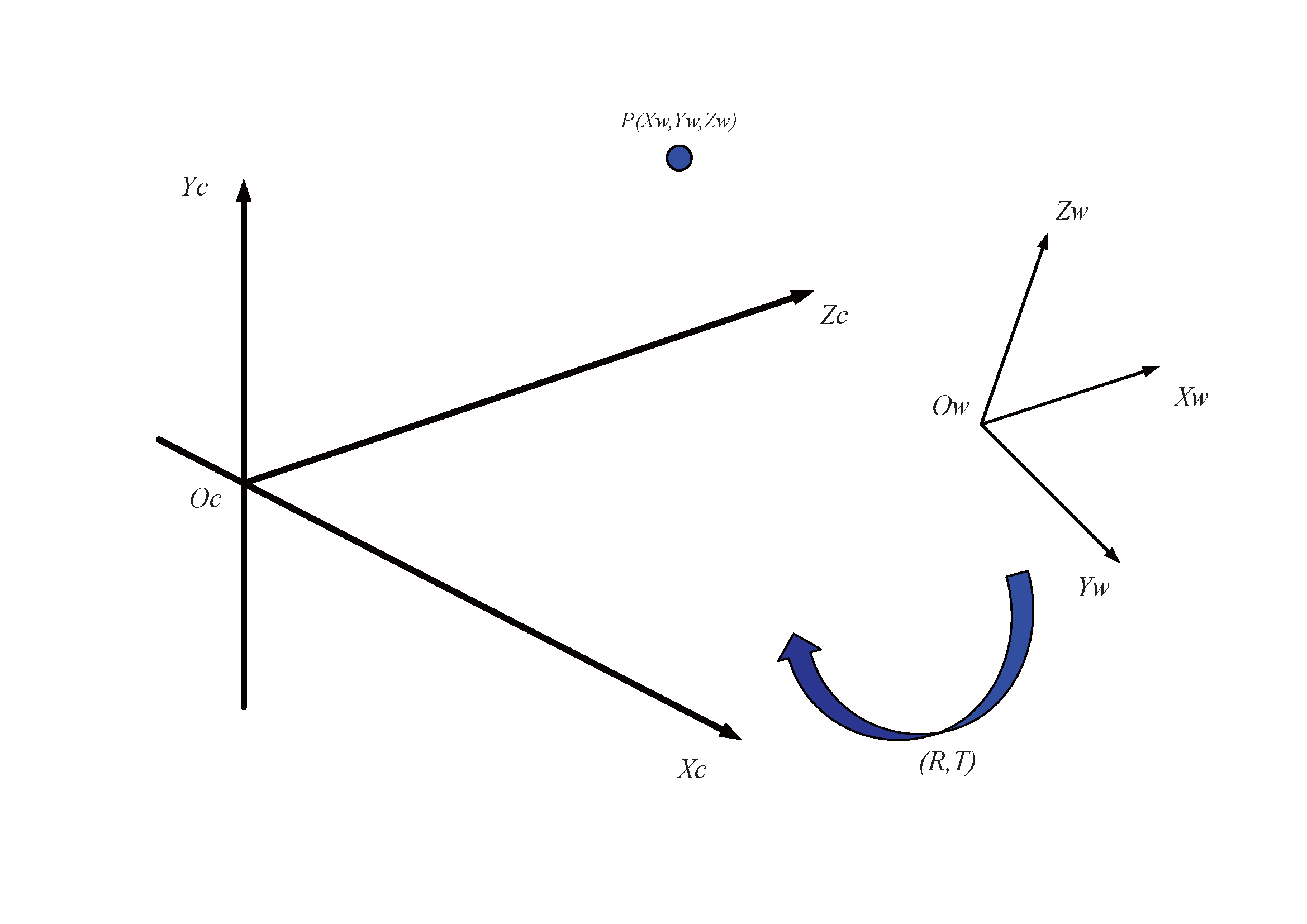
从世界坐标系变换到相机坐标系属于刚体变换:即物体不会发生形变,只需要进行旋转和平移。
$R$:表示旋转矩阵;
$T$:表示平移矩阵。
$$\left[\begin{matrix}X_c\\ Y_c \\Z_c\end{matrix}\right] = R \left[\begin{matrix} X_w \\Y_w \\Z_w\end{matrix}\right]+T$$
以齐次坐标表示:
$$\left[\begin{matrix}X_c\\ Y_c \\Z_c\\1\end{matrix}\right] = \left[\begin{matrix}R_{3\times 3}& T_{3\times 1}\\ 0 & 1\end{matrix}\right] \left[\begin{matrix} X_w \\Y_w \\Z_w\\1 \end{matrix}\right]$$
相机坐标系到图像坐标系之间的转换
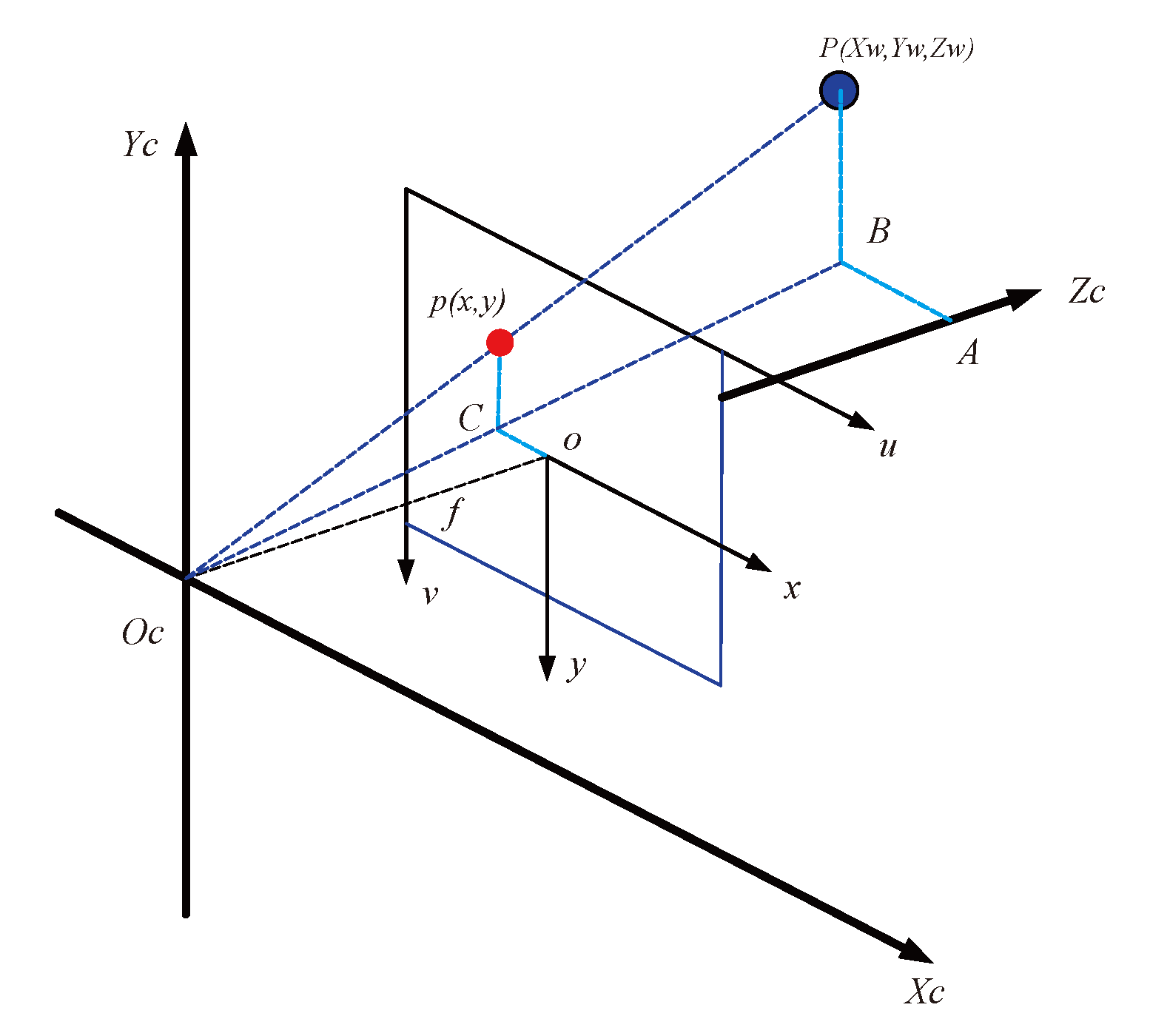
从相机坐标系到图像坐标系是从3D转换到2D,属于透视投影关系,以下是推导过程:
$\triangle ABO_c\sim\triangle oCO_c$
$\triangle PBO_c\sim\triangle pCO_c$
$$\frac{AB}{oC}=\frac{AO_c}{oO_c}=\frac{PB}{pC}=\frac{X_c}{x}=\frac{Z_c}{f}=\frac{Y_c}{y}$$
$$x=f\frac{X_c}{Z_c},y=\frac{Y_c}{Z_c}$$
$$Z_c\left[\begin{matrix}x\\ y\\ 1\end{matrix}\right]=\left[\begin{matrix}f&0&0&0\\ 0&f&0&0\\ 0&0&1&0\end{matrix}\right]\left[\begin{matrix}X_c\\ Y_c\\ Z_c\\ 1\end{matrix}\right]$$
很明显,$Z_c$是空间点$P$的深度信息。此时,投影点$p$的单位还是mm,并不是像素pixel,需要进一步转换到像素坐标系。
图像坐标系到像素坐标系之间的转换
像素坐标系和图像坐标系都在成像平面上,只是各自的原点和度量单位不一样。图像坐标系的原点为相机光轴与成像平面的交点,通常情况下是成像平面的中点或者叫principal point。图像坐标系的单位是mm,是物理单位,而像素坐标系的单位是pixel,我们平常描述一个像素点都是几行几列。所以这两者之间的转换关系如下: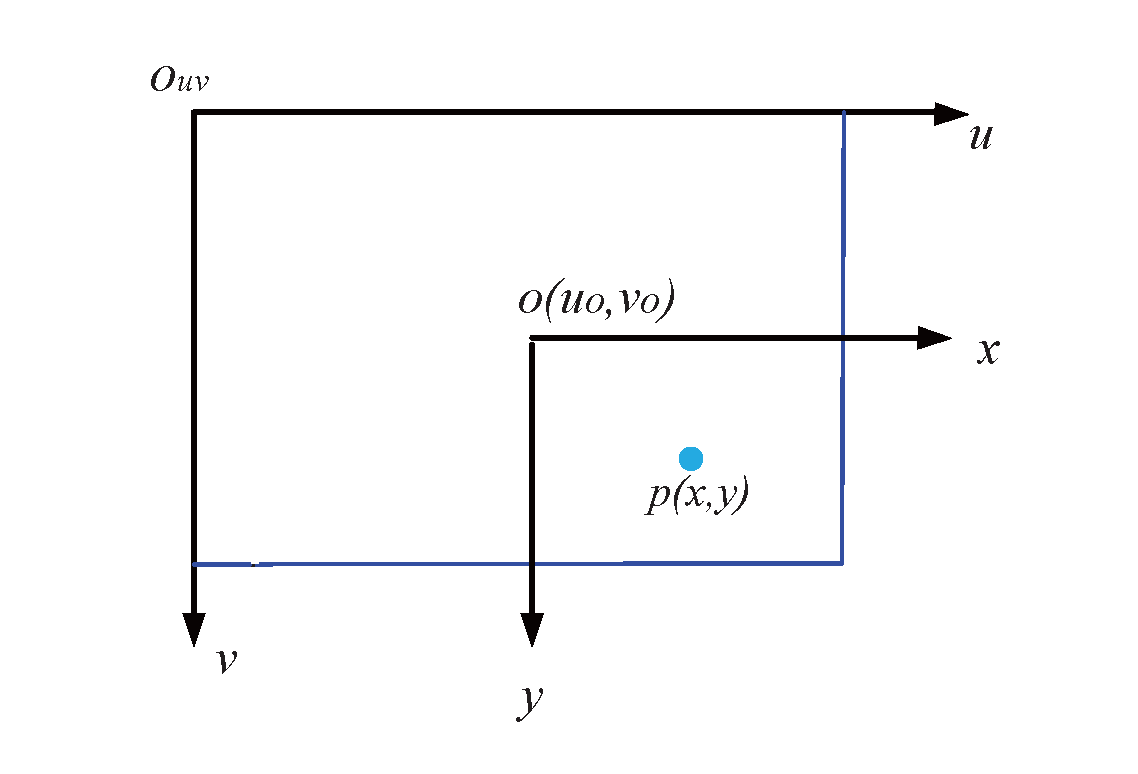
$$u=\frac{x}{dx}+u_0$$
$$v=\frac{y}{dy}+v_0$$
其中,$dx$和$dy$分别表示每一列和每一行分别代表多少mm,即$1pixel = dx mm$。
以齐次坐标形式表示为:
$$\left[\begin{matrix}u\\ v\\ 1\end{matrix}\right] = \left[\begin{matrix}\frac{1}{dx} & 0 &u_0\\ 0&\frac{1}{dy}& v_0\\0& 0& 1\end{matrix}\right]\left[\begin{matrix}x\\ y\\ 1\end{matrix}\right]$$
最后总结起来:
\begin{align}
Z_c\left[\begin{matrix}u\\ v\\ 1\end{matrix}\right]
&=\left[\begin{matrix}\frac{1}{dx} & 0 &u_0\\ 0&\frac{1}{dy}& v_0\\0& 0& 1\end{matrix}\right]\left[\begin{matrix}f&0&0&0\\ 0&f&0&0\\ 0&0&1&0\end{matrix}\right]\left[\begin{matrix}R_{3\times 3}& T_{3\times 1}\\ 0 & 1\end{matrix}\right]\left[\begin{matrix} X_w \\Y_w \\Z_w\\1 \end{matrix}\right]\\
&=\left[\begin{matrix}f_x&0&u_0&0\\ 0&f_y&v_0&0\\ 0&0&1&0\end{matrix}\right]\left[\begin{matrix}R_{3\times 3}& T_{3\times 1}\\ 0 & 1\end{matrix}\right]\left[\begin{matrix} X_w \\Y_w \\Z_w\\1 \end{matrix}\right]
\end{align}
其中,
$\left[\begin{matrix}f_x&0&u_0&0\\ 0&f_y&v_0&0\\ 0&0&1&0\end{matrix}\right]$为相机内参。
$\left[\begin{matrix}R_{3\times 3}& T_{3\times 1}\\ 0 & 1\end{matrix}\right]$为相机外参。
$Z_c$是深度信息:
所以一个空间中的坐标点,可以在图像中找到一个对应的像素点,但是,通过图像中的一个点找到它在空间中对应的点就很难。因为$Z_c$(深度信息)未知。
----------------------
以上(相机的内参和外参)都可以通过张正友标定获取。
----------------------

