本文主要记录卡尔曼滤波的推导过程,此记。
概念
卡尔曼滤波,首先说一下,为什么要用“滤波”这个词?
从带有噪声的数据中找到“最优估计”的过程就是“过滤”掉噪声的过程。
卡尔曼滤波是最好的线性估计方法。
建立系统数学模型
在实际应用中,我们可以将物理系统的运行过程看作是一个状态转换过程,卡尔曼滤波将状态空间理论引入到对物理系统的数学建模过程中来,其假设系统状态可以用$n$维空间的一个向量$X\in R^n$来表示。为了描述方便,我们作以下假设:1物理系统的状态转换过程可以描述为一个离散时间的随机过程;2系统状态受控制输入的影响;3系统状态及观测过程都不可避免受噪声影响;4对系统状态是非直接可观测的。
在以上假设前提下,定义系统状态变量为$x_k\in R^n$,系统控制输入为$u_k$,系统过程激励噪声为$w_k$,可得出系统的状态随机差分方程为:
$$x_k=Ax_{k-1}+Bu_{k-1}+w_{k-1}\tag{1}$$
定义观测变量$z_k\in R^m$,观测噪声为$v_k$,得到量测方程:
$$z_k=Hx_k+v_k\tag{2}$$
假设$w_k,v_k$为相互独立,正态分布的白色噪声,过程激励噪声协方差矩阵为$Q$,观测噪声协方差矩阵为$R$,即:
$$p(w)\sim N(0,Q)\tag{3}$$
$$p(v)\sim N(0,R)\tag{4}$$
$A,B,H$我们统称为状态变换矩阵,是状态变换过程中的调整系数,是从建立的系统数学模型中导出来的,这儿我们假设它们是常数。
滤波器计算原型
从建立的系统数学模型出发,可以导出卡尔曼滤波的计算原型,包括:时间更新方程和测量更新方程。 为了便于描述,做以下说明:(1)$\hat{x}_k\in R^n$,第$k$步之前的状态已知的情况下第$k$步的先验状态估计值($\bar{}$代表先验,$\hat{}$代表估计);(2)$\hat{x}_k\in R^n$ ,测量变量$z_k$已知情况下第$k$步的后验状态估计值。由此定义先验估计误差和后验估计误差:
$$e_k^{-}\equiv x_k-\hat{x}_k^{-}\tag{5}$$
$$e_k\equiv x_k-\hat{x}_k\tag{6}\label{pos_estim_error}$$
先验估计误差的协方差矩阵为:
$$P_k^{-}=E(e_k^{-}e_k^{-T})\tag{7}$$
后验估计误差的协方差矩阵为:
$$P_k=E(e_ke_k^{T})\tag{8}\label{pos_estim_error_conv}$$
先验估计$\hat{X}_k^{-}$和加权的测量变量$Z_k$及其预测$H\hat{X}_k^{-}$之差的线性组合构成了后验状态估计$\hat{X}_k$:
$$\hat{x}_k=\hat{x}_k^{-}+K(z_k-\hat{x}_k^{-})\tag{9}\label{pos_estim}$$
式中测量变量及其预测值之差$(z_k-\hat{X}_k^{-})$ 反映了预测值和实际值之间的不一致程度,称为测量过程的残余。残余为零表明二者完全吻合。$n\times m$阶矩阵$K$叫做残余的增益 ,作用是使\eqref{pos_estim_error_conv}式中的后验估计误差协方差最小。 可以通过以下步骤求出 K:将\eqref{pos_estim}式代入\eqref{pos_estim_error}式代入\eqref{pos_estim_error_conv}式,将$P_k$对$K$求导,使一阶导数为零,可以求出 $K$,$K$的一种形式为:
$$K_k = P_k^{-}H^T(HP_k^{-}H^T+R)^{-1}\tag{10}\label{kalman_k}$$
卡尔曼滤波器用反馈控制的方法估计过程状态: 滤波器估计过程某一时刻的状态, 然后以(含噪声的) 测量变量的方式获得反馈。 因此卡尔曼滤波器可分为两个部分: 时间更新方程和测量更新方程。 时间更新方程负责及时向前推算当前状态变量和误差协方差估计的值, 以便为下一个时间状态构造先验估计。 测量更新方程负责反馈――也就是说, 它将先验估计和新的测量变量结合以构造改进的后验估计。时间更新方程也可视为预估方程, 测量更新方程可视为校正方程。 最后的估计算法成为一种具有数值解的预估-校正算法, 如下图所示。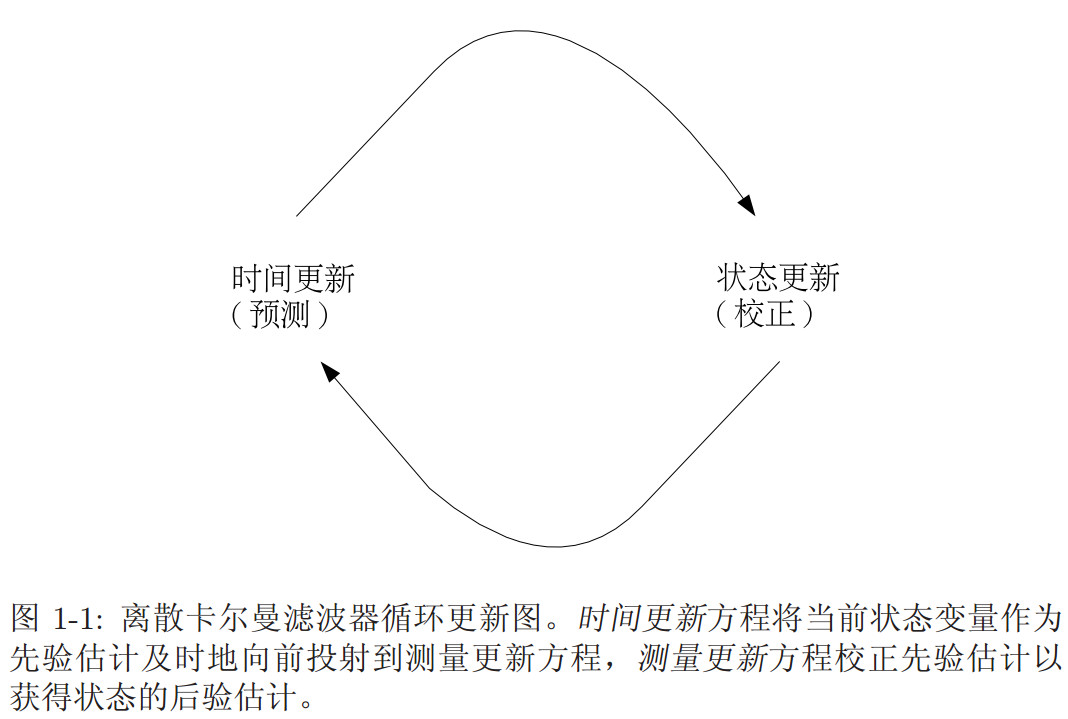
离散卡尔曼滤波器时间更新方程:
$$\hat{x}k^{-} = A\hat{x}{k-1}+Bu_{k-1}\tag{11}$$
$$P_k^{-} = AP_{k-1}A^T + Q\tag{12}$$
离散卡尔曼滤波器状态更新方程:
$$K_k = P_k^{-}H^T(HP_k^{-}H^T+R)^{-1}\tag{13}\label{kalman_gain}$$
$$\hat{x}_k=\hat{x}_k^{-}K_k(z_k - H\hat{x}_k^{-})\tag{14}\label{pos_estim2}$$
$$P_k = (I-K_kH)P_k^{-}\tag{15}\label{pos_cov}$$
测量更新方程首先做的是计算卡尔曼增益 $K_k$ 。 注意\eqref{kalman_gain}式和\eqref{kalman_k}式是相同的。 其次便测量输出以获得$z_k$, 然后按\eqref{pos_estim2}式(与\eqref{pos_estim}式相同) 产生状态的后验估计。 最后按\eqref{pos_cov}式估计状态的后验协方差。
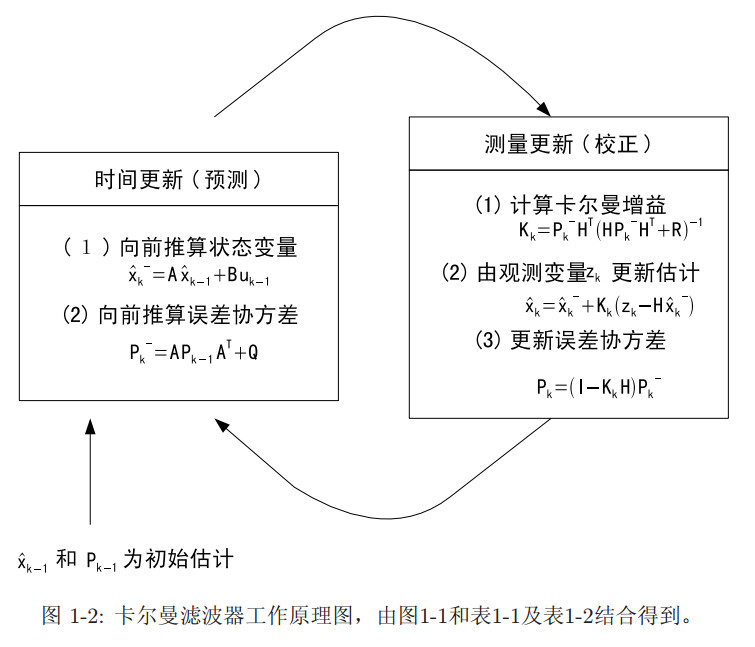
最后,滤波器的整个操作流程如下图所示: