本文主要讲述等效轴角坐标系表示法的导出过程,其中涉及到罗德里格斯公式(Rodrigues’ rotation formula)的推导,此记。
首先将坐标系 $B$ 和一个已知参考坐标系 $A$ 重合。将 $B$ 绕矢量 $^A\hat{K}$ 按右手定则旋转 $\theta$ 角度。
等效旋转矩阵的表示形式推导:
目标:将向量 $v=(x,y,z)$ 绕一般方向(而不是主轴方向) $\hat{r}$ (假设 $\hat{r}$ 是单位向量,如果不是,先进行单位化)旋转 $\theta$ 角度,如图1所示。
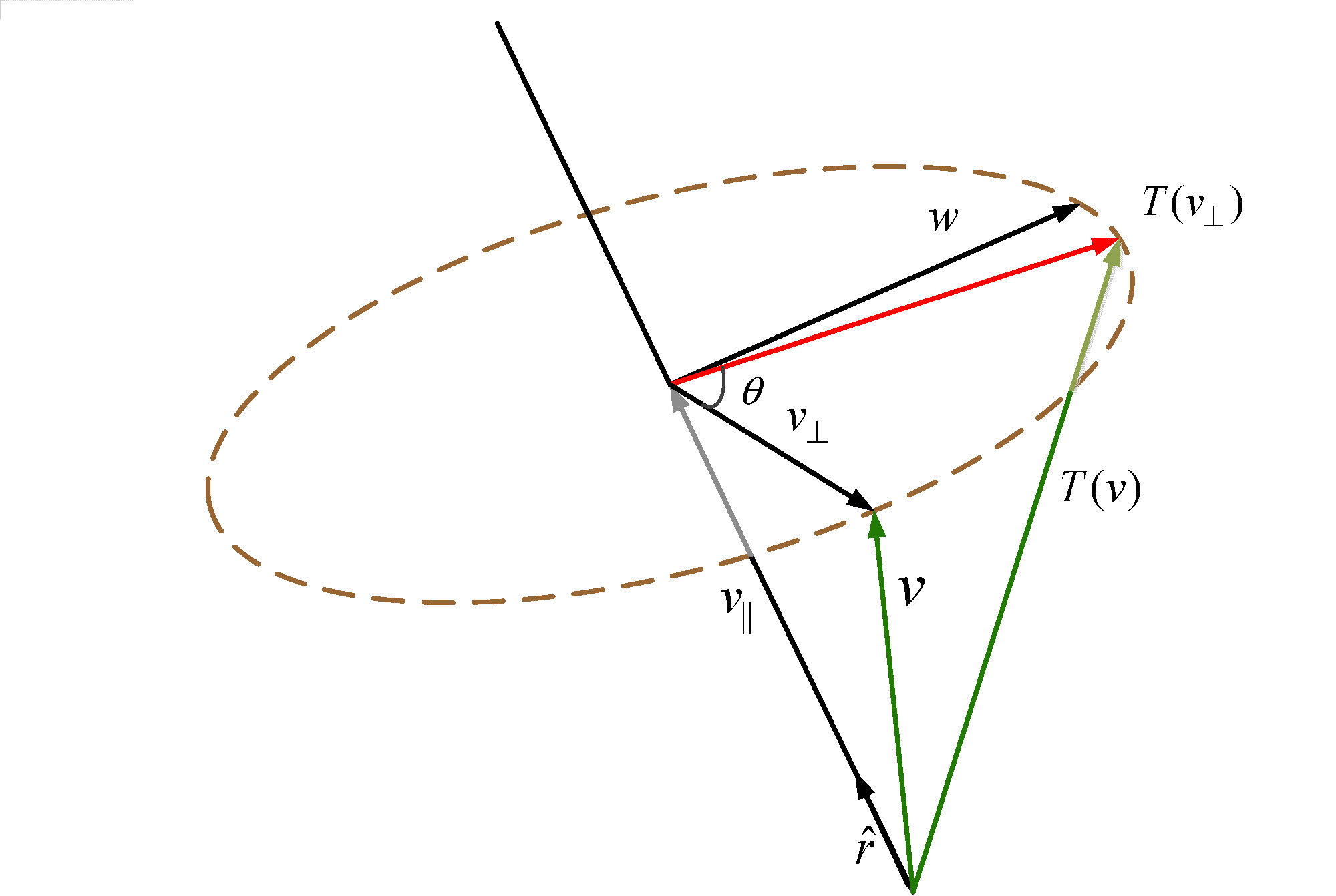
首先,将向量 $v$ 分解为两部分:平行于 $\hat{r}$ 的 $v_{||}$ 和垂直于 $\hat{r}$ 的 $v_{\bot}$,并且很容易可以得到:
$$v_{||}=(v\cdot \hat{r})\hat{r}$$
$$v=v_{||}+v_{\bot}$$
$$v_{\bot}=v-v_{||}$$
$$v_{\bot}=v-(v\cdot \hat{r})\hat{r}$$
假设,$T$ 是我们所要研究的旋转,我们需要计算 $T(v)$:
\begin{align}
T(v) & =T(v_{||}+v_{\bot})\\
& = T(v_{||})+T(v_{\bot})
\end{align}
因为 $v_{||}$ 平行于旋转轴 $\hat{r}$ ,所以
$$T(v_{||})=v_{||}$$
可以得到:
$$T(v)=v_{||}+T(v_{\bot})$$
其中, $T(v_{\bot})$ 是唯一需要求解的量。所以我们建立旋转平面上的两个基向量(如下图),把 $v_{\bot}$ 作为第一个基向量,第二个基向量用
\begin{align}
w & =\hat{r}\times v_{\bot}\\
& = \hat{r}\times v
\end{align}
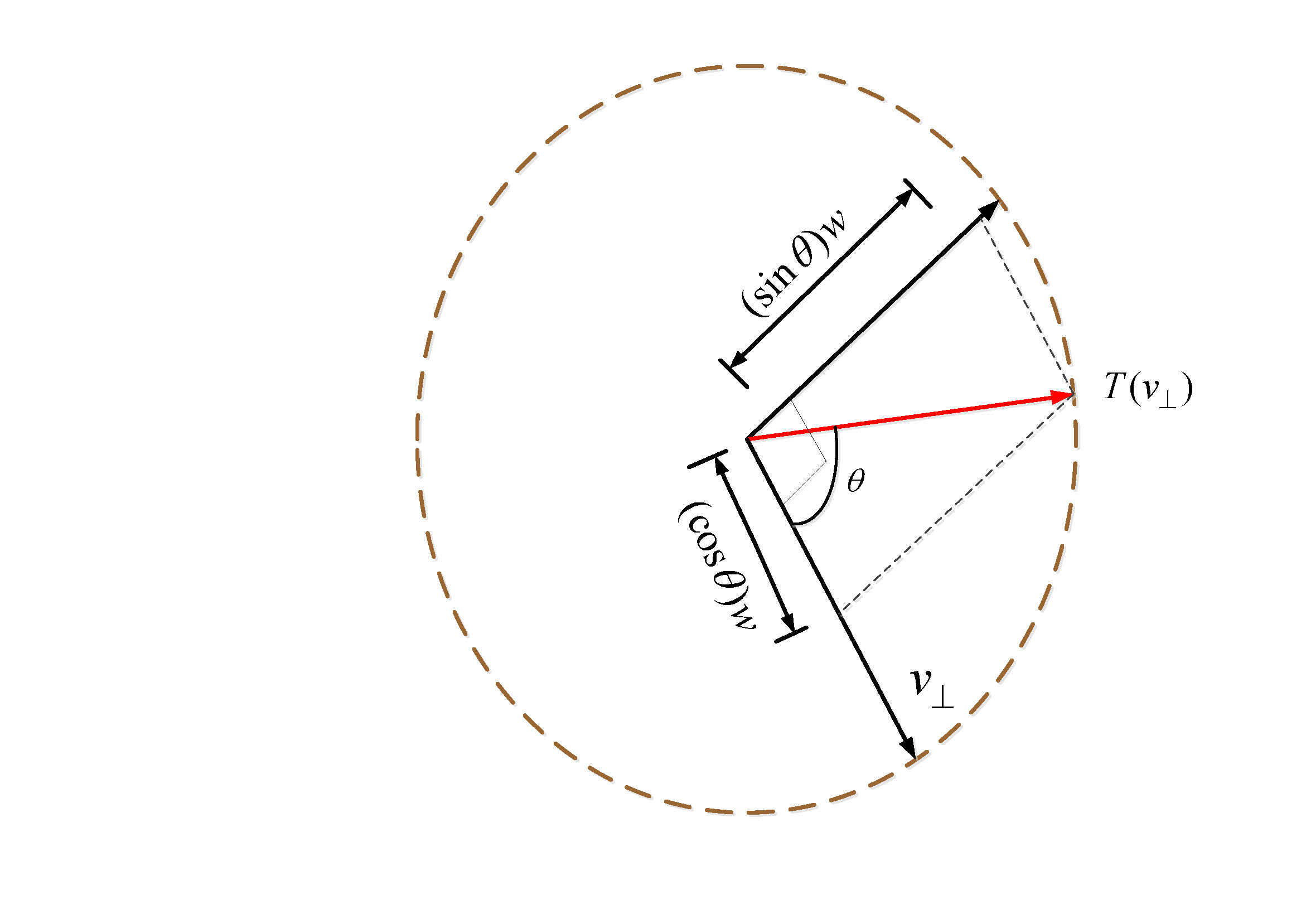
根据图2,我们可以得到:
\begin{align}
T(v_{\bot}) & = v_{\bot}cos\theta+ w sin\theta\\
&= v_{\bot}cos\theta+(\hat{r}\times v)sin\theta
\end{align}
因此,
\begin{align}
T(v) & =v_{||}+T(v_{\bot})\\
&=(v\cdot \hat{r})\hat{r}+ v_{\bot}cos\theta+ (\hat{r}\times v)sin\theta\\
&=(v\cdot \hat{r})\hat{r}+ [v-(v\cdot \hat{r})\hat{r}]cos\theta+(\hat{r}\times v)sin\theta\\
&=(v\cdot \hat{r})\hat{r}+ vcos\theta- (v\cdot \hat{r})\hat{r}cos\theta+ (\hat{r}\times v)sin\theta\\
&=(1-cos \theta)(v\cdot \hat{r})\hat{r}+ v cos\theta+ (\hat{r}\times v)sin\theta\end{align}
得到的该式为Rodrigues公式:
$$T(v)=(1-cos \theta)(v\cdot \hat{r})\hat{r}+ v cos\theta+ (\hat{r}\times v)sin\theta$$
至此,经过变换之后的向量形式已经表示出来了。可以分别通过三个基向量来求得等效旋转矩阵的一般形式:
$$p=\begin{vmatrix}1 &0 &0\end{vmatrix}^T $$
将向量 $p$ 绕轴 $\hat{r}=[k_x,k_y,k_z]$ 旋转(这里为了和参考书形式相同,采用 $k$ 表示)之后的形式表示为,
\begin{align}
p’ & =(1-cos \theta)(p\cdot \hat{r})\hat{r}+ pcos\theta+(\hat{r}\times p)sin\theta\\
&=(1-cos\theta)\left[\left(\begin{matrix}1\\0\\0\end{matrix}\right)\cdot \left(\begin{matrix}k_x\\k_y\\k_z\end{matrix}\right)\right]\left(\begin{matrix}k_x\\k_y\\k_z\end{matrix}\right)+\left(\begin{matrix}1\\0\\0\end{matrix}\right)cos\theta + \left[\left(\begin{matrix}k_x\\k_y\\k_z\end{matrix}\right)\times \left(\begin{matrix}1\\0\\0\end{matrix}\right)\right]sin\theta\\
&=\left[\begin{matrix}k_x^2(1-cos\theta)+cos\theta\\k_xk_y(1-cos\theta)+k_zsin\theta\\k_xk_z(1-cos\theta)-k_ysin\theta\end{matrix}\right]\end{align}
类似的,可以将 $q=\begin{vmatrix}0 &1 &0\end{vmatrix}^T$,$r=\begin{vmatrix}0 &0 &1\end{vmatrix}^T$ 经过旋转之后的形式表示为:
$$q’=\left[\begin{matrix}k_xk_y(1-cos\theta)-k_z sin\theta\\k_y^2(1-cos\theta)+cos\theta\\k_yk_z(1-cos\theta)+k_xsin\theta\end{matrix}\right]$$
$$r’=\left[\begin{matrix}k_xk_z(1-cos\theta)+k_y sin\theta\\k_yk_z(1-cos\theta)-k_xsin\theta\\k_z^2(1-cos\theta)+cos\theta\end{matrix}\right]$$
最后,可以得到等效旋转阵的形式:
$$R_r(\theta)=\left[\begin{matrix}k_x^2v\theta+c\theta&k_xk_yv\theta-k_zs\theta&k_xk_zv\theta+k_ys\theta\\k_xk_yv\theta+k_zs\theta&k_y^2v\theta+c\theta&k_yk_zv\theta-k_xs\theta\\k_xk_zv\theta-k_ys\theta&k_yk_zv\theta+k_xs\theta&k_z^2v\theta+c\theta\end{matrix}\right]$$
其中, $c\theta=cos\theta$ , $s\theta=sin\theta$ , $v\theta=1-cos\theta$ ,$\theta$ 是由右手定则确定的,即大拇指指向 $\hat{r}$ 的正方向。

